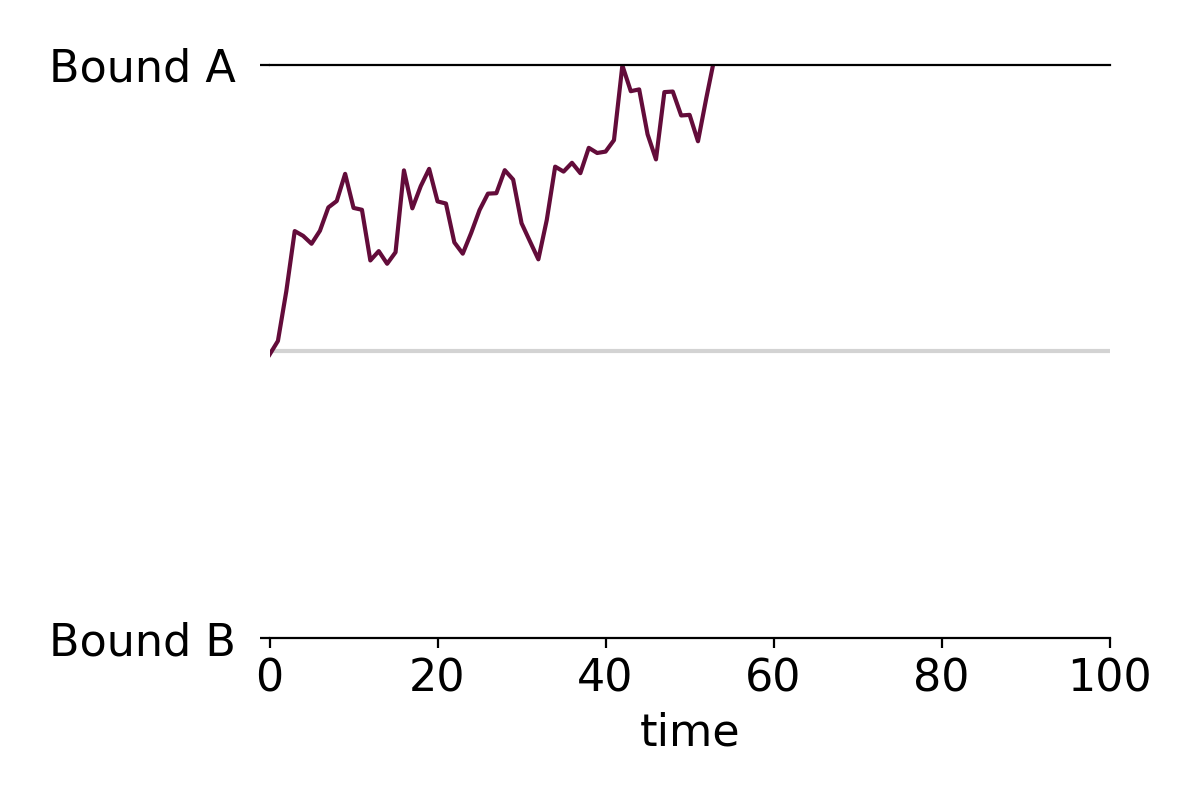
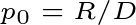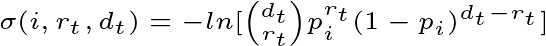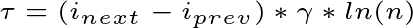This post contains a simple function that creates formatted drift-diffusion plots using matplotlib in Python. Drift-diffusion plots show how something "drifts" between two bounds over time. They're commonly used to visualize how people reach decisions after accumulating information. Here's an example of a drift-diffusion plot showing the average "drift" of multiple trials or instances:
I wrote this function when I was analyzing data from one of my experiments. In the experiment, participants had to guess which of two options was correct based on a stream of incoming evidence. The drift-diffusion plots represented their guesses (ranging from 100% certain option A was correct to 100% certain option B was correct) over time.
You can view and download the Jupyter notebook I made to create the plots here.
First, we'll import libraries, define some formatting, and create some data to plot.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
#set font size of labels on matplotlib plots
plt.rc('font', size=16)
#define a custom palette
customPalette = ['#630C3A', '#39C8C6', '#D3500C', '#FFB139']
plt.rcParams['axes.prop_cycle'] = plt.cycler(color=customPalette)
t = 100 #number of timepoints
n = 20 #number of timeseries
bias = 0.1 #bias in random walk
#generate "biased random walk" timeseries
data = pd.DataFrame(np.reshape(np.cumsum(np.random.randn(t,n)+bias,axis=0),(t,n)))
data.head()
DRIFT-DIFFUSION PLOT FUNCTION
def drift_diffusion_plot(values, upperbound, lowerbound,
upperlabel='', lowerlabel='',
stickybounds=True, **kwargs):
"""
Creates a formatted drift-diffusion plot for a given timeseries.
Inputs:
- values: array of values in timeseries
- upperbound: numeric value of upper bound
- lowerbound: numeric value of lower bound
- upperlabel: optional label for upper bound
- lowerlabel: optional label for lower bound
- stickybounds: if true, timeseries stops when bound is hit
- kwargs: https://matplotlib.org/api/_as_gen/matplotlib.pyplot.plot.html
Output:
- ax: handle to plot axis
"""
#if bounds are sticky, hide timepoints that follow the first bound hit
if stickybounds:
#check to see if (and when) a bound was hit
bound_hits = np.where((values>upperbound) | (values<lowerbound))[0]
#if a bound was hit, replace subsequent values with NaN
if len(bound_hits)>0:
values = values.copy()
values[bound_hits[0]+1:] = np.nan
#plot timeseries
ax = plt.gca()
plt.plot(values, **kwargs)
#format plot
ax.set_ylim(lowerbound, upperbound)
ax.set_yticks([lowerbound,upperbound])
ax.set_yticklabels([lowerlabel,upperlabel])
ax.axhline(y=np.mean([upperbound, lowerbound]), color='lightgray', zorder=0)
ax.set_xlim(0,len(values))
ax.set_xlabel('time')
ax.spines['left'].set_visible(False)
ax.spines['right'].set_visible(False)
return ax
PLOT A SINGLE TIME SERIES WITHOUT STICKY BOUNDS
You can specify if the plot should have sticky bounds or not. Setting stickybounds=TRUE prevents the time series from moving away from a bound once it is reached. This is equivalent to forcing "decisions" to be final. Setting stickybounds=FALSE allows the time series to move away from a bound.
ax = drift_diffusion_plot(data.iloc[:,4], upperbound=10, lowerbound=-10,
upperlabel='Bound A ', lowerlabel='Bound B ',
stickybounds=False)
PLOT A SINGLE TIME SERIES WITH STICKY BOUNDS (DEFAULT)
ax = drift_diffusion_plot(data.iloc[:,4], upperbound=10, lowerbound=-10,
upperlabel='Bound A ', lowerlabel='Bound B ')
CUSTOMIZE FORMATTING
You can customize the plot in several ways. First, you can pass in any of the kwarg arguments accepted by Matplotlib in the drift_diffusion_plot function. Here's a list of arguments you can pass in. Second, the function returns a handle to the plot's axis that you can use to further adjust the formatting.
#you can pass in any of the kwargs that matplotlib accepts
ax = drift_diffusion_plot(data.iloc[:,4], upperbound=10, lowerbound=-10,
stickybounds=False,
lw=2.5, ls=':', color=customPalette[1])
#return the axis to make additional changes
ax.set_xlabel(''); #remove x label
ax.set_xticks([0,31,59,90]) #adjust x ticks
ax.set_xticklabels(['Jan','Feb','Mar','Apr'], #change x tick labels
size=14, color='gray');
ax.set_yticklabels(['BUY ','SELL ']) #add y tick labels
ax.set_ylabel('price') #add y label
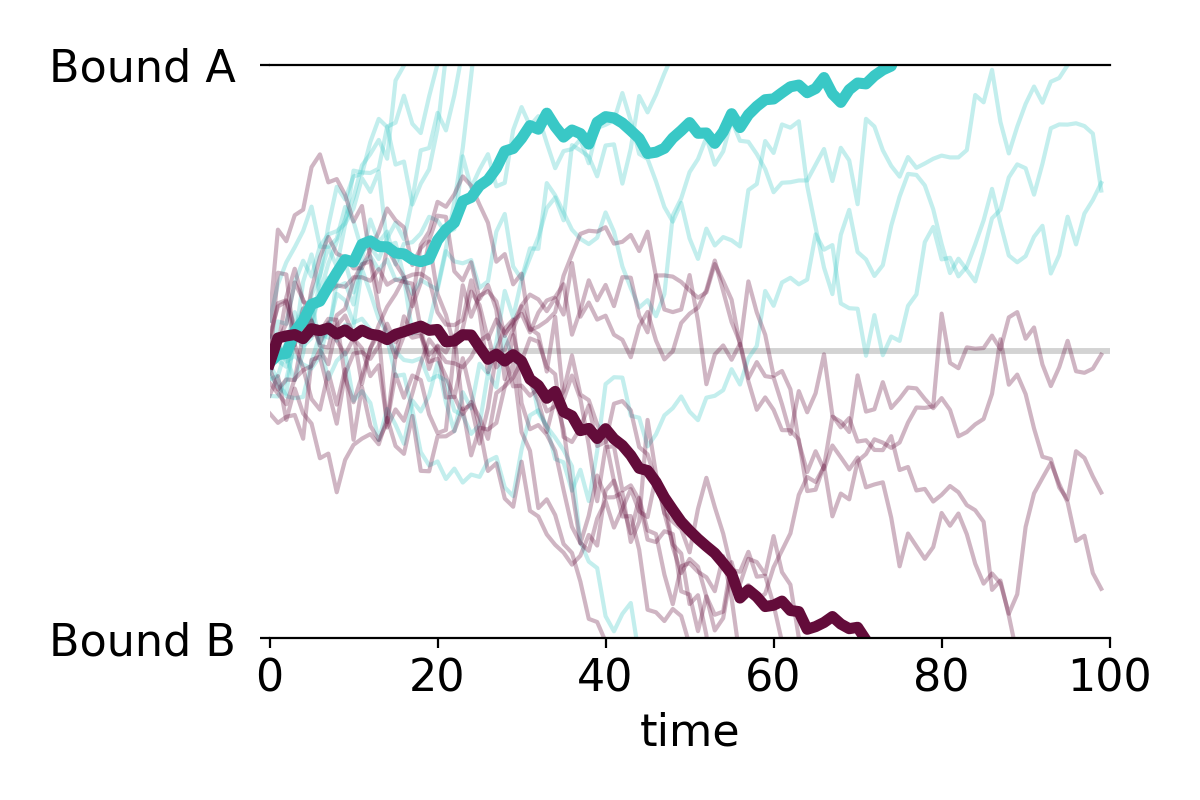
PLOT MULTIPLE TIME SERIES AND OVERLAY THE MEAN
You can easily apply the function to multiple time series. For example, making a plot with all individual time series along with the mean time series takes only two lines of code:
#plot individual timeseries
data.apply(drift_diffusion_plot, upperbound=10, lowerbound=-10, color='black', alpha=0.2);
#plot mean timeseries
drift_diffusion_plot(np.mean(data, axis=1), upperbound=10, lowerbound=-10,
upperlabel='Bound A ', lowerlabel='Bound B ',
color='black', lw=3);
PLOT MULTIPLE GROUPS
We can also plot the individual time series in two or more color-coded groups.
n=10
#group 1 (positive drift)
data1 = pd.DataFrame(np.reshape(np.cumsum(np.random.randn(t,n)+bias,axis=0),(t,n)))
data1.apply(drift_diffusion_plot, upperbound=10, lowerbound=-10,
color=customPalette[1], alpha=0.3);
drift_diffusion_plot(np.mean(data1, axis=1), upperbound=10, lowerbound=-10,
color=customPalette[1], lw=4, alpha=1);
#group 2 (negative drift)
data2 = pd.DataFrame(np.reshape(np.cumsum(np.random.randn(t,n)-bias,axis=0),(t,n)))
data2.apply(drift_diffusion_plot, upperbound=10, lowerbound=-10,
color=customPalette[0], alpha=0.3);
drift_diffusion_plot(np.mean(data2, axis=1), upperbound=10, lowerbound=-10,
upperlabel='Bound A ', lowerlabel='Bound B ',
color=customPalette[0], lw=4, alpha=1);
How to make arrow plots that visualize change
After a quick Google search, I realize that there may not be such a thing as an arrow plot and I may have made up the term. Regardless of whether it's an actual type of plot or not, I've found them useful in visualizing changes in some variable across individuals and this post describes how to make them in Python.
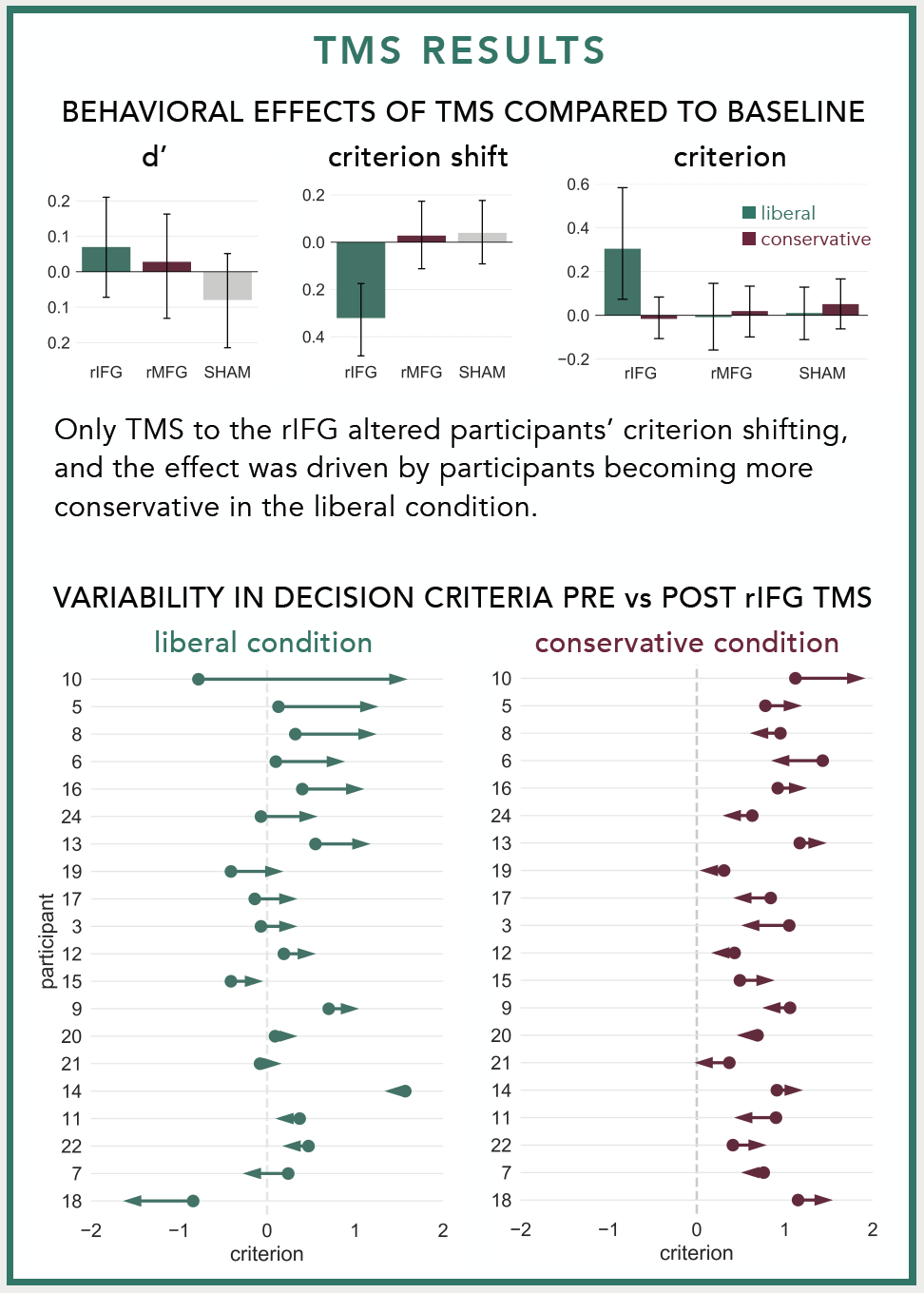
I first made the plot when I was trying to illustrate the variability in individuals' responses to neurostimulation. At the group level, our lab found that stimulating the right inferior frontal gyrus with repetitive Transcranial Magnetic Stimulation made participants more cautious to identify previously studied faces during a recognition memory experiment. We only observed this pattern in one condition and I wanted to visualize how participants' decision criteria changed before vs. after TMS in each condition. Normally I would use a strip plot with different colored points for before vs. after stimulation, but I thought replacing the points with an arrow pointed in the direction of the change would make for a simpler, more intuitive plot. Here's what the arrow plots looked like in the poster:
The dots in the arrow plots denote the participants' decision criteria before stimulation and the tip of the arrow heads denote their decision criteria after stimulation.
I use these plots often to visualize changes in participants' behaviors before vs. after neurostimulation, but they can be used in any situation where you need to illustrate how some variable changed among different entities. For example, you could use them to show how population changed among different US states, how mean salaries changed among different occupations, or how stock prices changed among different corporations.
You can view and download the Jupyter notebook I made to create the plots here.
First, we'll import libraries, define some formatting, and create some data to plot.
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import matplotlib.colors
%matplotlib inline
#set font size of labels on matplotlib plots
plt.rc('font', size=16)
#set style of plots
sns.set_style('white')
n = 30 #number of subjects
#create dataframe
data = pd.DataFrame(columns=['subject','before','after','change'], index=range(n))
data.loc[:,'subject'] = range(n)
data.loc[:,'before'] = np.random.normal(0, 0.5, n)
data.loc[:,'after'] = np.random.normal(0.25, 0.5, n)
data.loc[:,'change'] = data['after'] - data['before']
data.head()
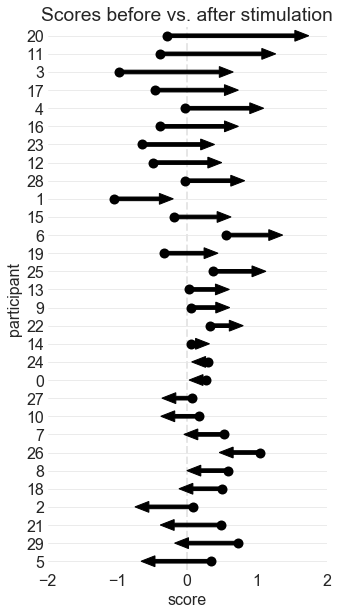
ARROW PLOT 1: BEFORE vs. AFTER VALUES
This is the same arrow plot I made for the ICB poster. The arrows start at the "before score" and end at the "after score." The participants are sorted according to how much their scores changed.
#sort individuals by amount of change, from largest to smallest
data = data.sort_values(by='change', ascending=False) \
.reset_index(drop=True)
#initialize a plot
ax = plt.figure(figsize=(5,10))
#add start points
ax = sns.stripplot(data=data,
x='before',
y='subject',
orient='h',
order=data['subject'],
size=10,
color='black')
#define arrows
arrow_starts = data['before'].values
arrow_lengths = data['after'].values - arrow_starts
#add arrows to plot
for i, subject in enumerate(data['subject']):
ax.arrow(arrow_starts[i], #x start point
i, #y start point
arrow_lengths[i], #change in x
0, #change in y
head_width=0.6, #arrow head width
head_length=0.2, #arrow head length
width=0.2, #arrow stem width
fc='black', #arrow fill color
ec='black') #arrow edge color
#format plot
ax.set_title('Scores before vs. after stimulation') #add title
ax.axvline(x=0, color='0.9', ls='--', lw=2, zorder=0) #add line at x=0
ax.grid(axis='y', color='0.9') #add a light grid
ax.set_xlim(-2,2) #set x axis limits
ax.set_xlabel('score') #label the x axis
ax.set_ylabel('participant') #label the y axis
sns.despine(left=True, bottom=True) #remove axes
ARROW PLOT 2: NORMALIZED CHANGES
This plot visualizes the change in scores, and not the scores themselves. It's effective if you want to emphasize the magnitude of change, and not the actual start points or end points. It looks cleaner, but it also conveys less information.
#sort individuals by amount of change, from largest to smallest
data = data.sort_values(by='change', ascending=True) \
.reset_index(drop=True)
#initialize a plot
fig, ax = plt.subplots(figsize=(5,10))
ax.set_xlim(-1.5,1.5)
ax.set_ylim(-1,n)
ax.set_yticks(range(n))
ax.set_yticklabels(data['subject'])
#define arrows
arrow_starts = np.repeat(0,n)
arrow_lengths = data['change'].values
#add arrows to plot
for i, subject in enumerate(data['subject']):
ax.arrow(arrow_starts[i], #x start point
i, #y start point
arrow_lengths[i], #change in x
0, #change in y
head_width=0.6, #arrow head width
head_length=0.2, #arrow head length
width=0.2, #arrow stem width
fc='black', #arrow fill color
ec='black') #arrow edge color
#format plot
ax.set_title('Changes in scores') #add title
ax.axvline(x=0, color='0.9', ls='--', lw=2, zorder=0) #add line at x=0
ax.grid(axis='y', color='0.9') #add a light grid
ax.set_xlim(-2,2) #set x axis limits
ax.set_xlabel('change') #label the x axis
ax.set_ylabel('participant') #label the y axis
sns.despine(left=True, bottom=True) #remove axes
ARROW PLOT 3: COLOR-CODED ARROWS
You can also color-code the arrows to illustrate positive or negative change:
#sort individuals by amount of change, from largest to smallest
data = data.sort_values(by='change', ascending=True) \
.reset_index(drop=True)
#initialize a plot
fig, ax = plt.subplots(figsize=(5,10)) #create figure
ax.set_xlim(-2,2) #set x axis limits
ax.set_ylim(-1,n) #set y axis limits
ax.set_yticks(range(n)) #add 0-n ticks
ax.set_yticklabels(data['subject']) #add y tick labels
#define arrows
arrow_starts = np.repeat(0,n)
arrow_lengths = data['change'].values
#add arrows to plot
for i, subject in enumerate(data['subject']):
if arrow_lengths[i] > 0:
arrow_color = '#347768'
elif arrow_lengths[i] < 0:
arrow_color = '#6B273D'
else:
arrow_color = 'black'
ax.arrow(arrow_starts[i], #x start point
i, #y start point
arrow_lengths[i], #change in x
0, #change in y
head_width=0.6, #arrow head width
head_length=0.2, #arrow head length
width=0.2, #arrow stem width
fc=arrow_color, #arrow fill color
ec=arrow_color) #arrow edge color
#format plot
ax.set_title('Changes in scores') #add title
ax.axvline(x=0, color='0.9', ls='--', lw=2, zorder=0) #add line at x=0
ax.grid(axis='y', color='0.9') #add a light grid
ax.set_xlim(-2,2) #set x axis limits
ax.set_xlabel('change') #label the x axis
ax.set_ylabel('participant') #label the y axis
sns.despine(left=True, bottom=True) #remove axes
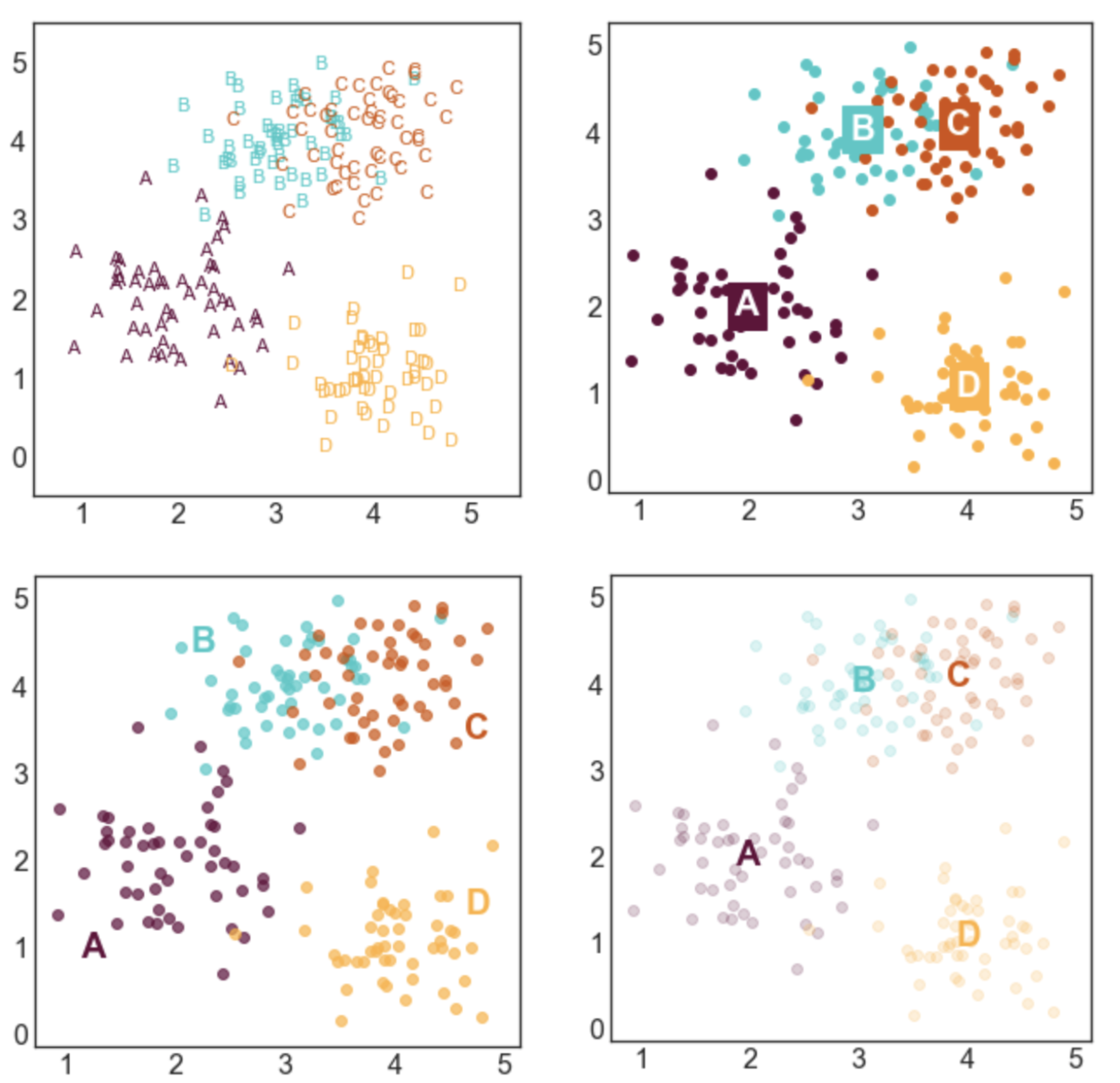
7 ways to label a cluster plot in Python
This tutorial shows you 7 different ways to label a scatter plot with different groups (or clusters) of data points. I made the plots using the Python packages matplotlib and seaborn, but you could reproduce them in any software. These labeling methods are useful to represent the results of clustering algorithms, such as k-means clustering, or when your data is divided up into groups that tend to cluster together.
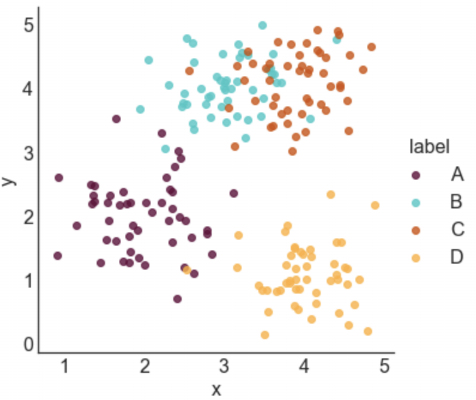
Here's a sneak peek of some of the plots:
You can access the Juypter notebook I used to create the plots here. I also embedded the code below.
First, we need to import a few libraries and define some basic formatting:
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
#set font size of labels on matplotlib plots
plt.rc('font', size=16)
#set style of plots
sns.set_style('white')
#define a custom palette
customPalette = ['#630C3A', '#39C8C6', '#D3500C', '#FFB139']
sns.set_palette(customPalette)
sns.palplot(customPalette)
CREATE LABELED GROUPS OF DATA
Next, we need to generate some data to plot. I defined four groups (A, B, C, and D) and specified their center points. For each label, I sampled nx2 data points from a gaussian distribution centered at the mean of the group and with a standard deviation of 0.5.
To make these plots, each datapoint needs to be assigned a label. If your data isn't labeled, you can use a clustering algorithm to create artificial groups.
#number of points per group
n = 50
#define group labels and their centers
groups = {'A': (2,2),
'B': (3,4),
'C': (4,4),
'D': (4,1)}
#create labeled x and y data
data = pd.DataFrame(index=range(n*len(groups)), columns=['x','y','label'])
for i, group in enumerate(groups.keys()):
#randomly select n datapoints from a gaussian distrbution
data.loc[i*n:((i+1)*n)-1,['x','y']] = np.random.normal(groups[group],
[0.5,0.5],
[n,2])
#add group labels
data.loc[i*n:((i+1)*n)-1,['label']] = group
data.head()
STYLE 1: STANDARD LEGEND
Seaborn makes it incredibly easy to generate a nice looking labeled scatter plot. This style works well if your data points are labeled, but don't really form clusters, or if your labels are long.
#plot data with seaborn
facet = sns.lmplot(data=data, x='x', y='y', hue='label',
fit_reg=False, legend=True, legend_out=True)
STYLE 2: COLOR-CODED LEGEND
This is a slightly fancier version of style 1 where the text labels in the legend are also color-coded. I like using this option when I have longer labels. When I'm going for a minimal look, I'll drop the colored bullet points in the legend and only keep the colored text.
#plot data with seaborn (don't add a legend yet)
facet = sns.lmplot(data=data, x='x', y='y', hue='label',
fit_reg=False, legend=False)
#add a legend
leg = facet.ax.legend(bbox_to_anchor=[1, 0.75],
title="label", fancybox=True)
#change colors of labels
for i, text in enumerate(leg.get_texts()):
plt.setp(text, color = customPalette[i])
STYLE 3: COLOR-CODED TITLE
This option can work really well in some contexts, but poorly in others. It probably isn't a good option if you have a lot of group labels or the group labels are very long. However, if you have only 2 or 3 labels, it can make for a clean and stylish option. I would use this type of labeling in a presentation or in a blog post, but I probably wouldn't use in more formal contexts like an academic paper.
#plot data with seaborn
facet = sns.lmplot(data=data, x='x', y='y', hue='label',
fit_reg=False, legend=False)
#define padding -- higher numbers will move title rightward
pad = 4.5
#define separation between cluster labels
sep = 0.3
#define y position of title
y = 5.6
#add beginning of title in black
facet.ax.text(pad, y, 'Distributions of points in clusters:',
ha='right', va='bottom', color='black')
#add color-coded cluster labels
for i, label in enumerate(groups.keys()):
text = facet.ax.text(pad+((i+1)*sep), y, label,
ha='right', va='bottom',
color=customPalette[i])
STYLE 4: LABELS NEXT TO CLUSTERS
This is my favorite style and the labeling scheme I use most often. I generally like to place labels next to the data instead of in a legend. The only draw back of this labeling scheme is that you need to hard code where you want the labels to be positioned.
#define labels and where they should go
labels = {'A': (1.25,1),
'B': (2.25,4.5),
'C': (4.75,3.5),
'D': (4.75,1.5)}
#create a new figure
plt.figure(figsize=(5,5))
#loop through labels and plot each cluster
for i, label in enumerate(groups.keys()):
#add data points
plt.scatter(x=data.loc[data['label']==label, 'x'],
y=data.loc[data['label']==label,'y'],
color=customPalette[i],
alpha=0.7)
#add label
plt.annotate(label,
labels[label],
horizontalalignment='center',
verticalalignment='center',
size=20, weight='bold',
color=customPalette[i])
STYLE 5: LABELS CENTERED ON CLUSTER MEANS
This style is advantageous if you care more about where the cluster means are than the locations of the individual points. I made the points more transparent to improve the visibility of the labels.
#create a new figure
plt.figure(figsize=(5,5))
#loop through labels and plot each cluster
for i, label in enumerate(groups.keys()):
#add data points
plt.scatter(x=data.loc[data['label']==label, 'x'],
y=data.loc[data['label']==label,'y'],
color=customPalette[i],
alpha=0.20)
#add label
plt.annotate(label,
data.loc[data['label']==label,['x','y']].mean(),
horizontalalignment='center',
verticalalignment='center',
size=20, weight='bold',
color=customPalette[i])
STYLE 6: LABELS CENTERED ON CLUSTER MEANS (2)
This style is similar to style 5, but relies on a different way to improve label visibility. Here, the background of the labels are color-coded and the text is white.
#create a new figure
plt.figure(figsize=(5,5))
#loop through labels and plot each cluster
for i, label in enumerate(groups.keys()):
#add data points
plt.scatter(x=data.loc[data['label']==label, 'x'],
y=data.loc[data['label']==label,'y'],
color=customPalette[i],
alpha=1)
#add label
plt.annotate(label,
data.loc[data['label']==label,['x','y']].mean(),
horizontalalignment='center',
verticalalignment='center',
size=20, weight='bold',
color='white',
backgroundcolor=customPalette[i])
STYLE 7: TEXT MARKERS
This style is a little bit odd, but it can be effective in some situations. This type of labeling scheme may be useful when there are few data points and the labels are very short.
#create a new figure and set the x and y limits
fig, axes = plt.subplots(figsize=(5,5))
axes.set_xlim(0.5,5.5)
axes.set_ylim(-0.5,5.5)
#loop through labels and plot each cluster
for i, label in enumerate(groups.keys()):
#loop through data points and plot each point
for l, row in data.loc[data['label']==label,:].iterrows():
#add the data point as text
plt.annotate(row['label'],
(row['x'], row['y']),
horizontalalignment='center',
verticalalignment='center',
size=11,
color=customPalette[i])
Detecting ‘bursts’ in time series data with Kleinberg’s burst detection algorithm
Awhile ago, I was watching an online course about data visualization and one of the analyses that stuck out to me was called burst detection. Burst detection is a way of identifying periods of time in which some event is unusually popular. In other words, you can use it to identify fads, or “bursts,” of events over time.
I realized that I could use burst detection to answer a long-standing curiosity of mine: what does a timeline of fMRI trends look like? What kind of fads have popped up in the short history of fMRI and what topics are currently popular? I have an intuitive sense of what topics were popular throughout fMRI's short history, but I like the idea of using burst detection to identify trends in the fMRI literature in a data-driven way.
The video that introduced me to the idea of burst detection used software that I didn’t have access to, but I found the paper that the analysis is based on, titled “Bursty and Hierarchical Structure in Streams”, by Kleinberg (2002). I implemented the bursting algorithm in Python, which you can access on Pypi or Github. The functions that I wrote apply to the algorithms described in the second half of the paper, which involve detecting bursts in discrete bundles of events. There are already packages in Python and R that implement the algorithms in the first half of the paper, which involve detecting bursts in continuous streams of events.
In this blog post, I will describe the rationale behind burst detection and describe how to implement it. In subsequent blog posts, I will apply the algorithm to real data. I’ve already found “bursts” in the fMRI literature and I’d like to also detect bursts in my Googling history and in news archives.
RATIONALE OF BURST DETECTION
Kleinberg’s burst detection algorithm identifies time periods in which a target event is uncharacteristically frequent, or “bursty.” You can use burst detection to detect bursts in a continuous stream of events (like receiving emails) or in discrete batches of events (like poster titles submitted to an annual conference). I focused on detecting bursts in discrete batches of events, since scientific articles are often published in batches in each journal issue.
Here’s the basic idea: a set of events, consisting of both target and non-target events, is observed at each time point t. If we use the poster title example, target events may consist of poster titles that include the word connectivity and non-target events may consist of all other poster titles (that is, all the poster titles that do not include the word connectivity). The total number of events at each time point is denoted by d and the number of target events is denoted by r. The proportion p of target events at each time point is equal to r/d.
Burst detection assumes that there are multiple states (or modes) that correspond to different probabilities of target events. Some states have high target probabilities, some states have very low target probabilities, and others have moderate target probabilities. If we assume that there are only two possible states, then we can think of the state with the lower probability as the baseline state and the state with the higher probability as the “bursty” state. The baseline probability is equal to the overall proportion of target events:
where R is the sum of target events at each time point and D is the sum of total events at each time point.
The bursty state probability is equal to the baseline probability multiplied by some constant s.You choose what to make s. If s is large, the probability of target events needs to be high to enter a bursty state.
When you are in a given state, you expect that, on average, the target events will occur with the probability associated with that state. Sometimes the proportion of target events will be higher than expected and sometimes it will be lower than expected due to random noise. The purpose of burst detection is to predict what state the system is in based on the sequence of observed proportions. In other words, given the observed proportions of target events in each batch of events, the burst detection algorithm will determine when the system was likely in a baseline state and when it was likely in a bursty state.
Determining which state the system is in at any given time depends on two things:
1. The goodness of fit between the observed proportion and the expected probability of each state. The closer the observed proportion is to the expected probability of a state, the more likely the system is in that state. Goodness of fit is denoted by sigma, which is defined as:
where i corresponds to the state (in a two-state system, i=0 corresponds to the baseline state and i=1 corresponds to the bursty state).
2. The difficulty of transitioning from the previous state to the next state. There’s a cost associated with entering a higher state, but no cost associated with staying in the same state or returning to a lower state. The transition cost, denoted by tau, therefore equals zero when transitioning to a lower state or staying in the same state. When entering a higher state, the transition cost is defined as:
where n is the number of time points and gamma is the difficulty of transitioning into higher states. You can choose the value of gamma. Higher values make it harder to transition into a more bursty state.
The total cost of transitioning from one state to another is equal to the sum of the two functions above. With the cost function in hand, we can find the optimal state sequence, q. The optimal state sequence is the sequence of states that minimizes the total cost or, in other words, the sequence that best explains the observed proportions. We find q with the Viterbi algorithm. The basic idea is simple: first, we calculate the cost of being in each state at t=1 and we choose the state with the minimum cost; then we calculate the cost of transitioning from our current state in t=1 to each possible state at t=2, and again we choose the state with the minimum cost. We repeat these steps for all time points to get a state sequence that minimizes the cost function.
The state sequence tells you when the system was in a heightened, or bursty, state. We can repeat these steps for different target events (for example, different words in poster titles) to build a timeline of what events were popular over time.
The strength, or weight, of a burst (that begins at time point t1 and ends at time point t2) can be estimated with the following function:
This equation simply tells us how much the fit cost is reduced when we are in a bursty state vs. the baseline state during the burst period. The more the fit cost is reduced, the stronger the burst and the greater the weight.
IMPLEMENTATION WITH SIMULATED DATA
I implemented the burst detection algorithm in Python and created a time series with artificial bursts to test the code. The time series consisted of 1000 time points and bursts were added from t=200 to t=399 and t=700 to t=799. Here’s what the raw time course looked like:
Setting s to 2 and gamma to 1, the algorithm identified one burst from t=701 to t=800 and 32 small bursts between t=200 and t=395. What does this tell us? The burst detection algorithm can easily identify periods in which the proportion of target events is much higher than usual, but it has a harder time identifying weaker bursts, especially in the presence of noise. I repeated the analysis using different values for s and gamma to get a sense of how these values affect the burst detection. Here, the bursts from each analysis (represented with blue bars) are plotted on the same timeline:
You can think of s as the distance between states. When s is small, the difference between the states’ expected probabilities is also small. When we increase s while holding gamma constant (as shown in the first four timelines), we get shorter bursts. Essentially, we’re breaking up larger bursts into smaller bursts since we’re increasing the threshold that the observed proportions need to meet in order to be considered in a burst. Since the time course is so noisy, some timepoints in the artificial burst periods do not meet that threshold and fewer and fewer time points meet the threshold as s increases.
Gamma determines how difficult it is to enter a higher state. Since there is no cost associated with staying in the same state or returning to a lower state, changing gamma should only affect the beginnings of bursts and not their endings. You can see that as gamma increases, we get fewer and shorter bursts since, again, we are making it more difficult to enter a bursty state. It’s not obvious from the timeline, but if you look at the start and end points of the burst that survived all of the gamma settings, you find that the burst ends at t=281 regardless of gamma. However, it begins at t=274 when gamma is 0.5, at t=279 when gamma is 1, and t=280 when gamma is 2 or 3.
As these plots illustrate, the burst detection algorithm is highly sensitive to noise. To reduce the effects of noise, we can temporally smooth the time course. Here’s what the bursts look like when we use a smoothing window with a width of 5 time points:
We get fewer, longer bursts since the proportions at each time point are less noisy. For this data, s=1.5 and gamma=1 identified both bursts.
Hopefully it’s obvious that the results of burst detection depend heavily on the parameters you choose. It may not be the best method to use if you care about the specific start and end points of bursts (or the number of bursts), but it’s a useful method if you’re interested in general trends in a large dataset over time.
I really recommend reading Kleinberg’s paper for a more detailed (and sophisticated) explanation of burst detection. If you’re interested in seeing the code I wrote to generate the figures in this post, you can check out my iPython notebook. The burst_detection package is my first, so please let me know if you run into any problems or if you notice any errors.
As I mentioned at the beginning of the post, I already applied the burst detection algorithm to the fMRI literature to identify trends in fMRI over the last 20 years. I’ll try to post that analysis soon. I have a few more project ideas after that, including finding trends in my Google search history, finding trends in rap lyrics, and finding trends in news articles. Let me know if you know of any interesting datasets that are amenable to burst detection or if you end up using the burst_detection package yourself.