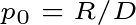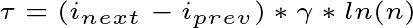30 years of trends in the MRI and fMRI literatures

When I entered graduate school, I knew next to nothing about functional magnetic resonance imaging (fMRI) and it's history. I eventually began to piece together a picture of fMRI's more recent history as I started to notice certain topics permeating conferences, classes, and conversations. Even so, I've long been curious about what topics shaped the fMRI and MRI literatures over time. When I learned about burst detection, I immediately wanted to use the method to create a data-driven timeline of fMRI. 

(You can view the Jupyter notebook I made to run all the analyses here. If you want to read more about burst detection, you can read this blog post, and if you want to apply burst detection analysis to your own data, you can download the burst detection package I compiled on PyPi.)

DATASET oF MRI ARTICLES

I used the PubMed database to collect the titles of MRI articles. I searched for the terms "fMRI" or "MRI" in the title/abstract field and restricted the results to articles and review papers published between 01/01/1987 and 11/30/17 and written in English. PubMed expanded the search to documents including the phrases "magnetic resonance imaging" or "functional magnetic resonance imaging" in the title or abstract. The search returned a total of 410,100 documents (accessed on 12/15/2017). 

I only kept articles with publication dates that included a month and a year. Articles that had no publication date at all, no publication month, a season rather than a month, or that were published outside the date range were discarded, leaving a total of 371,244 documents. 

If we look at how many MRI articles were published every month during the timeframe, we can see an almost linear (maybe exponential) increase in the number of articles published from 1987 to 2015, and then a slight decline. I don't know if this decline is due to some shift in the field -- maybe fewer articles contain the terms "fMRI" or "MRI" now or maybe fewer fMRI articles are being published -- or if it's reflective of some sort of delay in PubMed's indexing of articles. 

View fullsize

It looks like approximately (a whopping!) 2000 MRI and fMRI articles have been published every month since 2014. That is much more than I would have guessed. Granted, these may not all be actual MRI or fMRI studies. The search returned all documents that contained fMRI or MRI in the title or abstract, but it's unclear whether those articles published new results or simply referenced previous studies.

PREPROCESSING ARTICLE TITLES

Since this analysis tracks how often different words appear in MRI article titles over time, I first had to preprocess the titles in the dataset. Preprocessing was pretty minimal -- I simply converted all words to lowercase, stripped all punctuation, and split each title into individual words. The titles in the dataset contained 101,843 unique words. A large chunk of these words only appeared a few times. Since I'm interested in general trends, I don't really care about words that rarely appear in the literature. In order to weed out uncommon words and reduce computation time later on, I discarded all words that appeared fewer than 50 times in the dataset. That left 6,310 unique words.

I was curious about what words are used the most in MRI and fMRI article titles. Not surprisingly, some of the most common words were magnetic, resonance, and imaging (which were part of the search terms) and common articles and prepositions, such as the, of, and a. Ignoring these words, the most frequently used word in all MRI titles is.... brain! Also not very surprising. Here are the remaining 49 most common words in the dataset:

View fullsize

One thing about this list I found surprising is how medically-oriented most of the terms are. Since I'm surrounded by researchers who use fMRI to study cognition, I expected words like memory, executive, network, or activity to top the list, but they don't even appear in the top 50! I suspect there are two primary factors contributing to the medical nature of these words. First, the articles returned by searching for "MRI" are likely to be medical in nature since MRI has a myriad of medical imaging applications, including detecting tumors, internal bleeds, demyelination, and aneurysms. Accordingly, some of the most prevalent words reflect these applications, such as cancer, spinal, tumor, artery, lesions, sclerosis, cardiac, carcinoma, breast, stroke, cervical, and liver. Second, I used the full dataset -- which spanned 1987 to 2017 -- to identify the most common words, which biases terms that were prevalent throughout the full period. Since functional imaging didn't become widespread until a few years after anatomical imaging, it's less likely that functional-related terms would make into the most common words.

Next, I wanted to zoom in on MRI's more recent history and look at how the ranks of the most prevalent words changed over the last 10 years. I pulled out all article titles published since 2007 and found the top 15 most frequent words. Here are the counts of those top 15 words over the past 10 years:

This chart illustrates that the terms brain, patients, and study have been and still are the most popular words in fMRI and MRI article titles. In comparison, the popularity of case has declined over the last few years. In 2007, it was just as common as brain, patients, and study, but by 2017 it is used nearly 50% less often than these other terms. The terms disease, after, clinical, cancer, report, and syndrome all saw small dips after 2016 after long periods of continual increases, which may reflect the dip in the number of articles published in 2016 and 2017 (it may also reflect the fact that the data for 2017 doesn't include December). The term functional saw a large gain in the last 10 years, rising from the 9th spot in 2007 to the 4th spot in 2017. This may reflect the growing proportion of fMRI papers in the MRI literature or it may reflect the growing popularity of functional connectivity. 

FINDING FADS WITH BURST DETECTION

Looking at the most common words in the dataset gives us an idea about what topics are prevalent in the fMRI literature, but it doesn't give us a great idea about what topics are trending. For example, the word carcinoma appears in the dataset frequently, but its use hasn't really changed since 1987:

This differs from angiography and connectivity, which appear in the dataset about as frequently as carcinoma (the dotted lines represent the overall fraction of titles that contain each word), but are characterized by different time courses. Angiography was popular in the 1990s, but has since become less popular. In contrast, connectivity was virtually unused before 2005, but has since seen a meteoric rise. 

To find fads in the MRI literature, we can turn to burst detection. Burst detection finds periods of time in which a target is uncharacteristically popular, or, in other words, when it is "bursting." In our case, the target is one of the unique words in the dataset and we are looking for periods in which the word appears in a greater proportion of article titles than usual. The two-state model that I used assumes that a target can be in one of two states: a baseline state, in which the target occurs at some baseline or default rate, and a bursty state, in which the target occurs at an elevated rate. For every time point (in this case, for every month), the algorithm compares the frequency of the target at that time point to the frequency of the target over the full time period (the baseline rate) and tries to guess whether the target is in a baseline state or a bursty state. The algorithm returns its best guess of which state the target was in at each time point during the time period. In the example above, we would not expect carcinoma to enter a bursty state because the proportions don't get much greater than the baseline proportion (gray dotted line). However, we would expect connectivity to enter a burst state some time around 2014 because the proportions begin to far exceed the baseline proportion (blue dotted line).

There are a few parameters you can tweak in burst detection. The first is the "distance" between the baseline state and burst state. I used s=2 which means that a word has to occur with a frequency that is more than double its baseline frequency to be considered bursting. The second is the difficulty associated with moving up into a bursty state. I used gamma=0.5, which makes it relatively easy to enter a bursting state. Finally, I smoothed the time courses with a 5-month rolling window to reduce noise and facilitate the detection of the bursts. I applied the same burst detection model to all 6,310 unique words in the dataset to determine which terms, if any, were associated with bursts of activity and when those bursts occurred.

The vast majority of terms were not associated with any bursts, but a handful of terms did exhibit bursting activity. Below is a timeline of the top 100 bursts. Each bar represents one burst, with previous bursts in gray and current bursts (those that are still in a burst state as of November 2017) in blue. Since the time courses were smoothed, the start points and end points of the bursts are not precise (notice how the current bursts end in mid 2017). 

This analysis reveals a beautiful progression in the MRI literature. Imaging-related terms trend early on, with tomography, computed, resonance, mr, magnetic, nmr, nuclear, imaging, and ct bursting in the late 1980s and early 1990s. Medical terms begin to appear in the mid-1990s, including tumors, findings, evaluation, and angiography. The early 2000s are punctuated by advances in MRI technology, as demonstrated by bursts in the terms fast, three-dimensional, gamma, knife, event-related, and tensor. Bursts after 2010 capture the cognitive revolution ushered in by fMRI, with bursts in the terms cognitive, social, connectivity, resting, state, altered, network, networks, resting-state, default, and mode. 

To get an idea of how well the algorithm identified bursting periods, I plotted the proportions of the bursting words throughout the time period. Since there's great variability in the baseline proportions of the words, I normalized the monthly proportions by dividing them by each word's baseline proportion. Values of 1 indicate that the proportion is equal to the baseline proportion, values less that 1 (light blue) indicate that the proportion is less than the baseline, and values greater than 1 (dark blue) indicate that the proportion is greater than the baseline. The boundaries of the bursts are outline in black.

One thing that's apparent is that the burst detection algorithm does a poor job of detecting the beginning of the bursts. Take for example the terms fast, event-related, nephrogenic, state, pet/mr, and biomarker. I can think of a few explanations for this. First, it's possible that the algorithm identified multiple bursts, but the earlier bursts were not strong enough to enter the top 100 bursts. However, after looking at all of the bursts associated with the terms listed above, it doesn't look like any additional early bursts were detected. The second, more likely explanation, is that burst detection is simply ill-suited to detect early upticks in a topic. For example, if you look back to the time course of connectivity, it looks like the term begins to gain popularity around 2005 or so. However, up until 2011, the frequency of connectivity is less than the baseline frequency so the burst detection algorithm assumes it is in the baseline state. So instead of thinking of burst detection as a method that identifies when bubbles are forming, we should think of it as finding when bubbles burst or boil over (which is maybe when a fad starts anyway?)

CURRENT TRENDS

Since burst detection does a poor job of catching topics that are just beginning to become popular, I was curious about what topics are currently trending. To find the top trending words, I found the slope of the line of best fit of each word's proportions over the last two years. Words that appeared at the same rate throughout the time period should have slopes around zero, words that became less prevalent should have negative slopes, and words that became more prevalent should have positive slopes. After removing words with baseline proportions less than 0.005, I selected the top 15 words with the steepest upward slopes. The proportions of these words since 2015 is plotted below. (The trajectories are heavily smoothed to aid visualization, but they were not smoothed when computing the slopes.)

I think the lesson here is that if you want your research to be on the cutting edge, you need to write a paper titled "Accuracy and prognostic outcomes of simultaneous multi-parametric measurements for systematically predicting adolescents' resting-state networks and prostate cord fat." .... At least, I think that's the takeaway. 

Finally, here are the top 15 words that have been rising in popularity over a longer 15 year period:

Connectivity is the obvious break out star, appearing in less than 0.5% of articles in 2002 and nearly 4% of articles in 2017.

I could probably make another half dozen graphs, but I'll stop myself here. Let me know what you thought about this analysis or if you have ideas about additional things to look at. Next I'm going to work on applying the same analysis to identifying trends in the New York Times news article archive.

Detecting ‘bursts’ in time series data with Kleinberg’s burst detection algorithm

Awhile ago, I was watching an online course about data visualization and one of the analyses that stuck out to me was called burst detection. Burst detection is a way of identifying periods of time in which some event is unusually popular. In other words, you can use it to identify fads, or “bursts,” of events over time.

I realized that I could use burst detection to answer a long-standing curiosity of mine: what does a timeline of fMRI trends look like? What kind of fads have popped up in the short history of fMRI and what topics are currently popular? I have an intuitive sense of what topics were popular throughout fMRI's short history, but I like the idea of using burst detection to identify trends in the fMRI literature in a data-driven way.

The video that introduced me to the idea of burst detection used software that I didn’t have access to, but I found the paper that the analysis is based on, titled “Bursty and Hierarchical Structure in Streams”, by Kleinberg (2002). I implemented the bursting algorithm in Python, which you can access on Pypi or Github. The functions that I wrote apply to the algorithms described in the second half of the paper, which involve detecting bursts in discrete bundles of events. There are already packages in Python and R that implement the algorithms in the first half of the paper, which involve detecting bursts in continuous streams of events.

In this blog post, I will describe the rationale behind burst detection and describe how to implement it. In subsequent blog posts, I will apply the algorithm to real data. I’ve already found “bursts” in the fMRI literature and I’d like to also detect bursts in my Googling history and in news archives.

RATIONALE OF BURST DETECTION

Kleinberg’s burst detection algorithm identifies time periods in which a target event is uncharacteristically frequent, or “bursty.”  You can use burst detection to detect bursts in a continuous stream of events (like receiving emails) or in discrete batches of events (like poster titles submitted to an annual conference). I focused on detecting bursts in discrete batches of events, since scientific articles are often published in batches in each journal issue.

Here’s the basic idea: a set of events, consisting of both target and non-target events, is observed at each time point t. If we use the poster title example, target events may consist of poster titles that include the word connectivity and non-target events may consist of all other poster titles (that is, all the poster titles that do not include the word connectivity). The total number of events at each time point is denoted by d and the number of target events is denoted by r. The proportion p of target events at each time point is equal to r/d. 

Burst detection assumes that there are multiple states (or modes) that correspond to different probabilities of target events. Some states have high target probabilities, some states have very low target probabilities, and others have moderate target probabilities. If we assume that there are only two possible states, then we can think of the state with the lower probability as the baseline state and the state with the higher probability as the “bursty” state. The baseline probability is equal to the overall proportion of target events:

where R is the sum of target events at each time point and D is the sum of total events at each time point.

The bursty state probability is equal to the baseline probability multiplied by some constant s.You choose what to make s. If s is large, the probability of target events needs to be high to enter a bursty state.

When you are in a given state, you expect that, on average, the target events will occur with the probability associated with that state. Sometimes the proportion of target events will be higher than expected and sometimes it will be lower than expected due to random noise. The purpose of burst detection is to predict what state the system is in based on the sequence of observed proportions. In other words, given the observed proportions of target events in each batch of events, the burst detection algorithm will determine when the system was likely in a baseline state and when it was likely in a bursty state.

Determining which state the system is in at any given time depends on two things:

1. The goodness of fit between the observed proportion and the expected probability of each state. The closer the observed proportion is to the expected probability of a state, the more likely the system is in that state. Goodness of fit is denoted by sigma, which is defined as:

where i corresponds to the state (in a two-state system, i=0 corresponds to the baseline state and i=1 corresponds to the bursty state).

2. The difficulty of transitioning from the previous state to the next state. There’s a cost associated with entering a higher state, but no cost associated with staying in the same state or returning to  a lower state. The transition cost, denoted by tau, therefore equals zero when transitioning to a lower state or staying in the same state. When entering a higher state, the transition cost is defined as:

where n is the number of time points and gamma is the difficulty of transitioning into higher states. You can choose the value of gamma. Higher values make it harder to transition into a more bursty state.

The total cost of transitioning from one state to another is equal to the sum of the two functions above. With the cost function in hand, we can find the optimal state sequence, q.  The optimal state sequence is the sequence of states that minimizes the total cost or, in other words, the sequence that best explains the observed proportions. We find q with the Viterbi algorithm. The basic idea is simple: first, we calculate the cost of being in each state at t=1 and we choose the state with the minimum cost; then we calculate the cost of transitioning from our current state in t=1 to each possible state at t=2, and again we choose the state with the minimum cost. We repeat these steps for all time points to get a state sequence that minimizes the cost function.

The state sequence tells you when the system was in a heightened, or bursty, state. We can repeat these steps for different target events (for example, different words in poster titles) to build a timeline of what events were popular over time.

The strength, or weight, of a burst (that begins at time point t1 and ends at time point t2) can be estimated with the following function:

This equation simply tells us how much the fit cost is reduced when we are in a bursty state vs. the baseline state during the burst period. The more the fit cost is reduced, the stronger the burst and the greater the weight.

IMPLEMENTATION WITH SIMULATED DATA

I implemented the burst detection algorithm in Python and created a time series with artificial bursts to test the code. The time series consisted of 1000 time points and bursts were added from t=200 to t=399 and t=700 to t=799. Here’s what the raw time course looked like:

Setting s to 2 and gamma to 1, the algorithm identified one burst from t=701 to t=800 and 32 small bursts between t=200 and t=395. What does this tell us? The burst detection algorithm can easily identify periods in which the proportion of target events is much higher than usual, but it has a harder time identifying weaker bursts, especially in the presence of noise. I repeated the analysis using different values for s and gamma to get a sense of how these values affect the burst detection. Here, the bursts from each analysis (represented with blue bars) are plotted on the same timeline:

You can think of s as the distance between states. When s is small, the difference between the states’ expected probabilities is also small. When we increase s while holding gamma constant (as shown in the first four timelines), we get shorter bursts. Essentially, we’re breaking up larger bursts into smaller bursts since we’re increasing the threshold that the observed proportions need to meet in order to be considered in a burst. Since the time course is so noisy, some timepoints in the artificial burst periods do not meet that threshold and fewer and fewer time points meet the threshold as s increases.

Gamma determines how difficult it is to enter a higher state. Since there is no cost associated with staying in the same state or returning to a lower state, changing gamma should only affect the beginnings of bursts and not their endings. You can see that as gamma increases, we get fewer and shorter bursts since, again, we are making it more difficult to enter a bursty state. It’s not obvious from the timeline, but if you look at the start and end points of the burst that survived all of the gamma settings, you find that the burst ends at t=281 regardless of gamma. However, it begins at t=274 when gamma is 0.5, at t=279 when gamma is 1, and t=280 when gamma is 2 or 3.

As these plots illustrate, the burst detection algorithm is highly sensitive to noise. To reduce the effects of noise, we can temporally smooth the time course. Here’s what the bursts look like when we use a smoothing window with a width of 5 time points:

We get fewer, longer bursts since the proportions at each time point are less noisy. For this data, s=1.5 and gamma=1 identified both bursts.

Hopefully it’s obvious that the results of burst detection depend heavily on the parameters you choose. It may not be the best method to use if you care about the specific start and end points of bursts (or the number of bursts), but it’s a useful method if you’re interested in general trends in a large dataset over time.

I really recommend reading Kleinberg’s paper for a more detailed (and sophisticated) explanation of burst detection. If you’re interested in seeing the code I wrote to generate the figures in this post, you can check out my iPython notebook. The burst_detection package is my first, so please let me know if you run into any problems or if you notice any errors.

As I mentioned at the beginning of the post, I already applied the burst detection algorithm to the fMRI literature to identify trends in fMRI over the last 20 years. I’ll try to post that analysis soon. I have a few more project ideas after that, including finding trends in my Google search history, finding trends in rap lyrics, and finding trends in news articles. Let me know if you know of any interesting datasets that are amenable to burst detection or if you end up using the burst_detection package yourself.